Musical Numerology
By Don Robertson
(First published in 1970 in Don Robertson’s book Kosmon. Footnotes were added by Don Robertson in 2022)
“I wrote the article Musical Numerology in 1970 and published it in Denver, Colorado in a book called Kosmon, created and published by myself, my ex-wife and my friend John Fresques, who created the artwork. It was in this book that I first put forward my findings about what I was calling the duochord, and that rock and roll music was at that time at the beginning of a downward turn.
“One day, after we had started distributing the book to local bookstores, I received a letter from a young man who lived nearby and wanted to meet the author of this article. I went to see him. Looking around his one-bedroom apartment, I saw that everywhere there were large pieces of white paper on which he had been making mathematical calculations: spread across tables, chairs, and taped to all of the walls. He was ecstatic, “I had to meet the author because I have applied what was stated in the article to every known science and found that the same formula proves itself in every case.” I went back a week later to discuss the matter with him more thoroughly, but the apartment was empty. He was gone.
“Now after 23 years, I have revised the article, and am publishing it again on by educational site DoveSong.com. I hope this information can be as useful to others as it was for this young man and has been for me. I believe that musical scales and harmony are based on alchemical realities that can be proved by math. Math demonstrates the formation of the laws of the universe. Music, color, and all manifestation follow the same laws.”
— Don Robertson (May, 2003)
To our knowledge, there is no religion on the earth that does not incorporate a symbolic use of the quantities three and seven. Our objective is to illustrate some of the mysterious relationships between the quantities three and seven, and what these quantities have in common with the basic physical structure of the universe.
The direct relationship between three and seven is as follows: If we have three objects, which we will call 1, 2, and 3, we will observe that the absolute number of different combinations of these 3 objects is 7; that is, we may arrange them in no more than seven different combinations, regardless of the order in which they are arranged.
Combination 1 | 1, 2, 3 |
Combination 2 | 1, 2 |
Combination 3 | 1, 3 |
Combination 4 | 2, 3 |
Combination 5 | 1 |
Combination 6 | 2 |
Combination 7 | 3 |
The Color Spectrum
There are three primary colors in the color spectrum, plus four more natural colors that are created from the combinations of the three colors similarly to the three objects above. All colors that exist are either: a) One of the primary colors, or b) A resultant mixture of two or three of the primary colors. The primary colors cannot be created by mixing other colors, so they are rather special. The three primary colors are red, yellow, and blue.[1] The natural, or secondary colors are those colors that are created by mixing equally the three primary colors according to the chart above. The resultant seven natural colors the colors of the rainbow, a naturally occurring phenomena that can be created using a prism to break down light. They are arranged in the spectrum as follows:
Red | 1 | Red |
Orange | 1, 2 | Red, Yellow |
Yellow | 2 | Yellow |
Green | 2, 3 | Yellow, Blue |
Blue | 3 | Blue |
Indio | 1, 2, 3 | Red, Yellow, Blue |
Violet | 1, 3 | Red, Blue |
Thus, we see that the color spectrum is based on the relationship between 3 and 7.
[1] It is noted that modern theory of colors has adapted new colors to represent the subtractive domain of primary colors, and some writers go so far as to dispute the standard primary colors, but we stand by what we have written: red, yellow and blue are the primary colors.
The Musical Scale
There are three primary tones of the musical scale and seven natural tones:
C | 1 | C |
D | 1, 2 | C, E |
E | 2 | E |
F | 2, 3 | E, G |
G | 3 | G |
A | 1, 2, 3 | C, E, G |
B | 1, 3 | C, G |
The notes that correspond to the primary colors are C, E, G: the major triad, which is the most important chord in music and the groundwork of the scale. It is important to realize the correspondence between the colors of the spectrum and the notes of the scale, as the musical scale is based on the same principals of nature (the natural overtone series) and it has been adapted in some form or another in most all cultures.
There are three major triads contained in the major scale (C, D, E, F, G, A, B). These are: the major triad that is based on the correspondence with the primary colors (C, E, G) and two others (F, A, C and G, B, D). There are also three minor triads (D, F, A and E, G, B and A, C, E). Major and minor triads are the fundamental underpinnings of harmony, on which the music of Western cultures is based.
Three Forces at the Heart of Nature
The simplest physical structure in the material universe is the hydrogen atom. It has the least number of forces at work: it has only three forces. These are:
- At the center of the atom resides the nucleus, composed of a positive charge of electricity called a proton.
- Orbiting around this proton in an elliptical orbit is a negative charge of electricity called an electron. Since this electron has a negative charge, and since a negative charge is attracted to a positive charge, the electron is attracted to the proton.
- Since the electron is attracted to the proton, there must be a force that causes equilibrium between the two, as the electron would collide with the proton if no such force were in place. This force then is the force that governs bodies in motion, causing them to travel in an orbit. It is centrifugal force. In the atom, this is the neutron.
Some Aspects of Three
If there is a given object that is fixed in space, this object has, as its location, three coordinates. An example of this would be the relative position of an airplane above the earth. It is calculated by longitude, latitude, and altitude: its three coordinates.
If someone looks into the corner of a room, where the room meets the walls, they will see three intersecting planes that are considered to extend into infinity. These are the three dimensions of space.
There are three time zones that man senses, past, present, and future.
If there is space with no motion, then time does not exist, only space. But if there is no motion, then there can be no space, for there must be space to contain the motion. The motion through space causes sequentiality. The earth’s orbit around the sun and the revolution on its axis causes a time sequence on earth. Thus, we have three aspects: time, space, and motion.
The Law of Three
The fact that events, laws, and all creation result from three principals is referred to as the “Law of Three” or the “Law of the Triangle.” This law is illustrated by the example that every effect has two causes: one passive, and one active.
What does the Russian philosopher Georges Gurdieff have to say about the Law of Three? In the book In Search of the Miraculous, P.D. Ouspensky quotes him as follows: “This is the ‘Law of Three’ or the law of the three principles or the three forces. It consists of the fact that every phenomenon, on whatever scale and in whatever world it may take place, from molecular to cosmic phenomena, is the result of the combination or the meeting of three different and opposing forces. Contemporary thought realizes the existence of two forces and the necessity of these two forces for the production of a phenomenon: force and resistance, positive and negative magnetism, positive and negative electricity, male and female cells, and so on. But it does not observe even these two forces always and everywhere. No question has ever been raised as to the third, or if it has been raised it has scarcely been heard. “According to real, exact knowledge, once force, or two forces, can never produce a phenomenon. The presence of a third force is necessary, for it is only with the help of a third force that the first two can produce what may be called a phenomenon, no matter in what sphere. “The teaching of the three forces is at the root of all ancient systems. The first force may be called active or positive, the second, passive or negative; the third, neutralizing. But these are merely names; for in reality, all three forces are equally active and appear as active, passive and neutralizing, only at their meeting points, that is to say, only in relation to one another at a given moment. The first two forces are more or less comprehensible to man and the third may sometimes be discovered either at the point of application of the forces, or in the medium, or in the result. But speaking in general, the third forces is not easily accessible to direct observation and understanding. The reason for this is to be found in the functional limitations of man’s ordinary psychological actively and in the fundamental categories of our perception of the phenomenal world, that is, in our sensations of space and time resulting from these limitations. People cannot perceive and observe the third force directly any more than they can spatially perceive the fourth dimension. “The first fundamental law of the universe is the law of three forces, or three principles, or as it is often called, the law of three. According to this law, every action, every phenomenon in all worlds without exception, is the result of a simultaneous action of three forces: the positive, the negative, and the neutralizing. Of this we have already spoken…. The next fundamental law of the universe is the law of seven or the law of octaves.” |
Some Aspects of Seven
During the late 1700’s, some chemists began identifying certain chemical elements. About 1800, they began to determine the atomic weights of some of them. In 1808, John Dalton suggested that atoms were physical objects with specific weights. In 1829, Johann Doebereiner showed that elements could be arranged in groups of three. In each group, the elements had similar properties and the weight of the middle atom of the group was close to the average of the other two. These were said to be chemical equivalents to the musical triad.
The Law of Octaves
In 1864, John A. Newlands grouped all the known elements in the order of their atomic weights. He then divided them into groups of seven elements each. He showed that when the atoms were put in order with their weights increasing, there was a repetition in the similarities according to the musical octave, the same found on the keyboard. When he talked to chemists of this time about his newly found law of octaves, they laughed.
But octaves are the substance of the musical scale, the same musical scale that was demonstrated by Pythagoras and used today, with slight modifications according to culture. It is a naturally occurring phenomena. The basis of the musical scale is the octave, the repetition of the vibration of the set of seven notes that occurs when the fundamental vibration of the first note, the basic note of that scale, is doubled.
In 1869, Mendeleev compiled his famous Periodic Table of the Elements. This table was arranged according to atomic weights. Mendeleev found, as had Newlands, that the chemical properties of the elements reoccur at definite intervals. He concluded that these were the periodic functions of their atomic weights. According to Daniel Morris, in his article “Music of the New Spheres” in the December 1969 Chemistry Magazine, Mendeleev’s arrangement of the elements came to him while listening to a performance of Robert Schumann’s exquisite Piano Quintet, Opus 44. He was seated upon a sofa, apparently mulling over Newland’s and Doebereiner’s arrangements of the elements, when all of a sudden, he jumped up, sat at his desk, and arranged all of the elements accordng to a new plan. Morris’ feeling was that there was a definite relationship between the quintet and the periodic table in the repetition and development of the seven-note melody of the quintet.
Vibrations in Different Octaves
It was in 1925 that French scientist Louis Victor Pierre Raymond duc de Broglie discovered that the electron was a wave of vibration. These waves properly follow the same property and characteristics of vibration as the vibrating string of a musical instrument, the waves being complete with overtones. (We are familiar with the presence of overtones on the vibrating string from the experiments of Pythagoras and his monochord – a single-stringed instrument that he built to display how musical scales were produced by the natural overtone series).
An atom such as uranium has more that 90 electrons, each capable of its own harmonies. All this can be recorded by a spectroscope. One can conclude that all matter is made of waves. Therefore, we, and the world we live in, are vibrations…just as the children of the 1960s discovered while taking large doses of LSD! But this should not be too surprising. Our understanding of the world around us is through perception of the five senses. What we experience is taking place in our brain, interpretations of waves of light, taste, smell, feeling, and sound. Are we really living in a world, as we suspect, or is this simply a world created in our brain, like the experience that we have when we dream? And if spectral and aural vibrations obey the same law of octaves that applies to the physical makeup of the universe, then perhaps it is all just a part of one large keyboard of vibrations, with particular sensations and manifestations taking place in particular octave ranges. Light, heat, magnetic and chemical vibration are all subject to the law of octaves.
The ancient Greek philosopher Democritus wrote:[1]
Sweet and bitter – Cold and warm,
As well as all the colors.
All these things exist
But in opinion
And not in reality.
What really exists
Are unchangeable
articles: atoms,
And their motions in empty space.
The great German mathematician Gottfried Wilhelm Leibniz wrote: “I am able to prove that not only light, color, heat, and the like, but motion, shape and extension too are mere apparent qualities.” Many scientists and philosophers have concluded that everything exists in the mind: stars, planets, atoms. Einstein showed us that even space and time were forms of intuition.
Georges Gurdjieff, the important Russian spiritual teacher said that the law of octaves was based upon the discontinuity of all vibrations in nature, as they do not develop uniformly, but with periodic accelerations and retardations. The original impulse becomes alternately stronger and weaker. This is a phenomenon like the AC cycle. This cycle of alternating electrical vibrations can be viewed by means of an oscilloscope or with a computer program such as Sound Forge. Called the duty cycle, it appears as such:

All sounds are made up of these cycles, and they take place in what is called the time domain. By using a brilliant mathematical formula known as the Fourier transform, these cycles can be translated into the frequency domain, where we find that the timbre of the sound depends upon the strength of the sound’s overtones: the higher harmonics of the fundamental tone.
The duty cycle can be equated to a circle broken at its diameter with the bottom half twisted 180 degrees or to the continuous movement of a spiral. Alternating current (AC) obeys the laws of the duty cycle: energy alternates with no energy. Home electricity in the United States alternates sixty times per second, thus it is called 60 cycles, also known as 60 Hertz. An electric light bulb does not continually burn, but flashes sixty times in one second, faster than our eyes can follow, so we perceive the appearance of continuous light. This would not be the case when light is powered by a battery, as batteries produce direct current (DC), which does not alternate with a duty cycle.
Musical tones can be represented using the mathematical symbols of trigonometry, signs and cosigns, and the imaginary numbers of calculus. Computer systems that generate musical tones, such as synthesizers, do so using these mathematical formulas. All of this is based on the alternation of the duty cycle.
[1] νόμωι (γάρ φησι) γλυκὺ καὶ νόμωι πικρόν, νόμωι θερμόν, νόμωι ψυχρόν, νόμωι χροιή, ἐτεῆι δὲ ἄτομα καὶ κενόν (Tetralogies of Thrasyllus, 9; Sext. Emp. adv. math. VII 135)
“Shocks”
While teaching in Russia during the first world war, Gurdjieff described something about octaves that had not been publically known before. He stated that there were two places in the octave where retardation of the vibrations takes place. These places are between the notes E and F and between the notes B and C. These are the two places on the keyboard where there are no sharp or flat note (black) keys between the white keys. Octaves, according to Gurdjieff, develop according to whether these places where retardation of vibrations take place are “filled.” In the right development of these octaves, these places are filled by the energy of octaves that run in parallel to the given octave. Gurdjieff called this process of filling in, a shock. Processes, institutions, laws, businesses, and many other things all progress through time according to the law of octaves, and therefore these two shocks in the octave are a part of the development process. Gurdjieff stated that if development continues without the shocks being filled in, then the line of development constantly changes. The way he described it, if octaves – as a principal of nature – develop unimpeded, the development looks as if it is proceeding along a straight line, but every time one of the two points in the octave is reached where a shock occurs, even though development of the process that the octave represents appears to be progressing forward along a straight line, the development of the process actually jogs a little, causing what would be compared to a jog in the line. The development continues and after the progress through the series of octaves has gone on for a particular amount of time, what was considered to be development along a straight line has actually turned into a development in the opposite direction! Further continuation will bring the development back to the same direction that it started in, or a full revolution on a spiral.
The law of octaves, with this intrinsic circular motion generating a spiral, governs all activity and shows how organizations, religions, and governments — if allowed to develop without conscious knowledge concerning the application of the ‘filling in’ of these shocks — develop into something that is opposite to what was originally intended.
The Octave with Two Added Shocks
Gurdjieff explained how an octave of seven ‘notes’ is transformed from seven into nine – the seven notes and the two shocks – by applying the following fascinating bit of arithmetic.
He divided the number ‘1’ into seven equal fractions:
1/7 | 2/7 | 3/7 | 4/7 | 5/7 | 6/7 | 7/7 |
The decimal equivalents of these seven fractions are arrived at using the time-honored tradition of dividing the numerators by the denominator:
1/7 = | .142857 |
2/7 = | .285714 |
3/7 = | .428571 |
4/7 = | .571428 |
5/7 = | .714285 |
6/7 = | .857142 |
(Of course, 7/7 equals 1).
Studying the numbers that result from our division is a fascinating process. We find that we have a reoccurring sequence of numbers that is present in every case! This sequence is: 142857, which continues on and on ad infinitum.
.142857142857142857 etc….
7/1.00000000000000000
(Numerical patterns such as these are very telling. They describe a situation that is naturally occurring and should be taken seriously by the researcher).
The nature of this pattern is very interesting. If we start with the number ‘7’, which is the number of the octave, we see that the next number in line is double that number, ‘14’. Following that we have another doubling: ‘28’, and after that another doubling: ‘56’…whoops, not 56, but 57, the ‘7’ being the start of another sequence! It takes some thought about this to fully appreciate the beauty of this sequence and this change from 56 to 57 to start another series. This just really breathes “cycle,” does it not? There are other interesting things about this series of numbers. If we add each column in the set of six decimals above, we always get the number ‘27’ as a result. This is because each of the six decimal sequences is ordered in such a way that when you add downwards, only the six numbers of the sequence appear, there are no duplications. We have six pieces of the whole (7/7), each with a sequence of six numbers, the same sequence in each piece, ordered in the same unique fashion. This is something to contemplate.
Now we will turn to something called horizontal addition. This is a process used in numerology. Although we don’t endorse the common understanding of what numerology represents, the principles behind manipulation of numbers are simple aspects of natural mathematics that demonstrates the laws of nature, and this understanding of numbers and what they are all about holds the key to understanding nature, and what it is all about. That is why trigonometry and calculus are so important to engineering. Both these sciences give us an understanding of nature, and hence, an understanding of sound, and the natural laws that govern the use of sound in music…principals that are not arbitrary, but work according to natural law, the law of three, the law of octaves, and now the law of nine (the octave plus the two shocks).
By using horizontal addition on the sequence, we arrive at the number 27:
1 + 4 + 2 + 8 + 5 + 7 = 27
Adding the sequence numbers together, we end up with ‘9’. This demonstrates one way that seven ties into nine.
2 + 7 = 9
The Periodicity of Nine
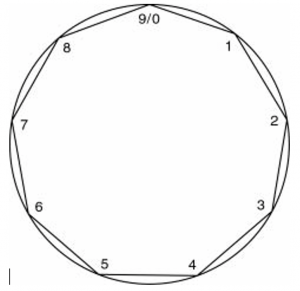
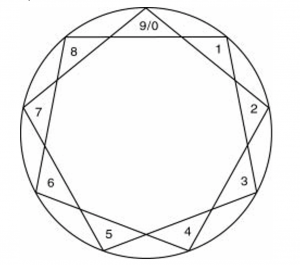
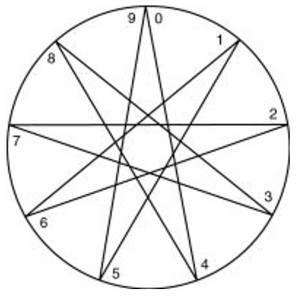
The notes of the octave combined with the two shocks demonstrate to us what is called the periodicity of nine. Creating a circle with nine positions and connecting the numbers from our sequence above, we have the figure that Gurdjieff calls an enneagram.
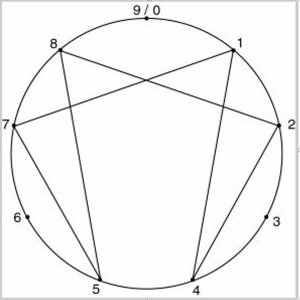
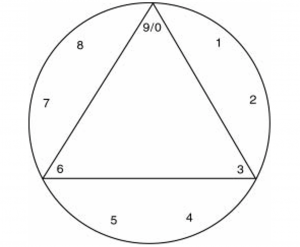
The numbers that are not in the sequence are 3, 6, and 9. When they are connected, the result is a triangle. The numbers 3 and 6 are the shocks.
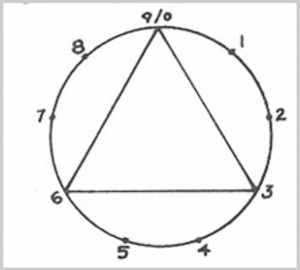
By applying the color spectrum and musical notes to the enneagram, we have the following:
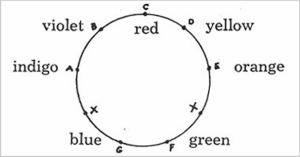
When asked why one shock correctly appears between the E and the F, but the other, instead of appearing between B and C, appears between G and A in the enneagram symbol, Gurdjieff stated that this demonstrated the nature of the shock that occurred when passing from one octave to the next.[1] He also said that every completed whole, every organism, is an enneagram, but that each of these enneagrams does not have an inner triangle (3,6,9). 142857 is the working of the corporeal scheme, the triangle is the presence of higher elements in the organism. This inner triangle is possessed by plants, for example, from which come our “drugs”: hemp, poppy, hops, tea, coffee, tobacco.[2]
When any number is added to nine, the sum, added horizontally to one significant figure, always equals that same number (also added horizontally to one significant figure).
Examples: | ||
8 + 9 = 17 | and | 1 + 7 = 8 |
6 + 9 = 15 | and | 1 + 5 = 6 |
36 + 9 = 45 | and | 4 + 5 = 9 and 3 + 6 = 9 |
When any number is multiplied by nine, the product added horizontally to one significant figure, always equals nine.
Examples: |
|
9 x 7 = 63 | |
9 x 12 = 108 | |
[1] “Perhaps the appearance of the shock between the note G and the note A demonstrates a tie between the major scale beginning on the note C and the relative minor scale that begins on A.
[2] According to the Theory of Nikola Tesla’s “Numbers 3, 6 and 9,” there are 9, and only nine, digital root numbers. All other higher or lower numbers are the combination of those digital root numbers. The famous Tesla quote is “If you only knew the magnificence of 3,6 and 9, then you would have a key to the universe.
Casting Out Nines
This interesting drawing shows how multiplication of nine by the other single-digit numbers produces a sum that fits nicely into our enneagram. We have equated nine with zero because nine becomes zero when it is cast. Notice how the sums are equal to the two numbers at that level of the drawing (for example, the sums on the first line are 18 and 81, on the second 72 and 27 and so on).
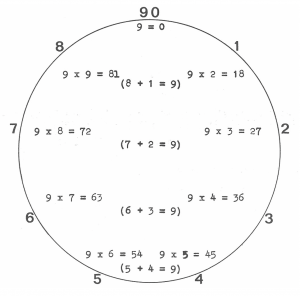
We see that by horizontal addition of the sums, in each case, we always end up with nine. If we now take each number from one to eight and multiply it by numbers 1 through 9 – we will see some interesting numerical patterns develop. We will start with the first line from the circle above:
8 x 1 = 8
8 x 2 = 7 (16, or 1 + 6 = 7)
8 x 3 = 6 (24, or 2 + 4 = 6, and so on…)
8 x 4 = 5
8 x 5 = 4
8 x 6 = 3
8 x 7 = 2
8 x 8 = 1
8 x 9 = 9
We end up now with a sequence of 876543219. A similar sequence is produced by doing the same thing with 1. This sequence is the reverse of the other:
1 x 1 = 1
1 x 2 = 2
1 x 3 = 3
1 x 4 = 4
1 x 5 = 5
1 x 6 = 6
1 x 7 = 7
1 x 8 = 8
1 x 9 = 9
This is how this sequence looks on the circle:
Notice that this sequence was generated by the numbers 8 and 1, the two numbers at the top of the enneagram. The number series that resulted from these two was the same, however one series is the reverse of the other. For 8 we have: 876543219, and for 1 we have 12345789. To be completely the opposite of each other, the second series would have had to have been 987654321, but interestingly enough, this isn’t the case.
Now we will generate another pair of sequences using seven and two, the next set of numbers in the enneagram.
7 x 1 = 7 7 x 2 = 5 7 x 3 = 3 7 x 4 = 1 7 x 5 = 8 7 x 6 = 6 7 x 7 = 4 7 x 8 = 2 7 x 9 = 9 | 2 x 1 = 2 2 x 2 = 4 2 x 3 = 6 2 x 4 = 8 2 x 5 = 1 2 x 6 = 3 2 x 7 = 5 2 x 8 = 7 2 x 9 = 9 |
This is how this sequence looks on the circle:
Again, we have a resultant series of numbers where one is the opposite of the other. For 7 we have 753186429, and for 2 we have 246813579. As is the case with 8 and 1 above, both series always ends with a 9! Also, the reverse series is one number off from the original. This series of numbers is one that skips every other number.
Now we will generate another pair of sequences using five and four:
5 x 1 = 5 5 x 2 = 1 5 x 3 = 6 5 x 4 = 2 5 x 5 = 7 5 x 6 = 3 5 x 7 = 8 5 x 8 = 4 5 x 9 = 9 | 4 x 1 = 4 4 x 2 = 8 4 x 3 = 3 4 x 4 = 7 4 x 5 = 2 4 x 6 = 6 4 x 7 = 1 4 x 8 = 5 4 x 9 = 9 |
This is how this sequence looks on the circle:
When we look at these, we see again that we have the same kind of pattern where the series from the second set is the opposite of the first, however offset by a single number, and that both end in 9. The series for 5 is 516273849 and the series for 4 is 483726159. This series of numbers is one where three numbers is skipped each time.
Finally, we will take a look at the sequence generated by the two shock values three and six:
6 x 1 = 6 6 x 2 = 3 6 x 3 = 9 6 x 4 = 6 6 x 5 = 3 6 x 6 = 9 6 x 7 = 6 6 x 8 = 3 6 x 9 = 9 | 3 x 1 = 3 3 x 2 = 6 3 x 3 = 9 3 x 4 = 3 3 x 5 = 6 3 x 6 = 9 3 x 7 = 3 3 x 8 = 6 3 x 9 = 9 |
This is how this sequence looks:
Interestingly enough, the number 6 yields a series of 639, 639, 639, and the series from 3 yields the opposite: 369, 369, 369. Who says the universe isn’t the result of mathematics!
We have now horizontally multiplied each number from 1 to 9 by the numbers 1 through 9 and have arrived at a series that is in each case has been illustrated using the enneagram circle, the circle with 9 points. The numbers 1,2,4,5,7, and 8 are the numbers found in the period (142857). When we look at the tables that we have just created using these numbers (that is the tables for “8 and 1”, “7 and 2”, and “5 and 4”) we can see that a series of numbers has been created in each table. For example, in the 8 table, the results from horizontally multiplying 1 through 9 by 8 resulted in a pattern (reading down the sum column) of 876543219 and the results from horizontally multiplying 7 by 1 through 9 is the sequence 753186429. Now, taking the third, sixth, and ninth numbers in each of these series, we discover that we have a repeating sequence of either 639 or 369. These are the “inner triangles” of each one of these sets:
8 x 1 = 8 8 x 2 = 7 8 x 3 = 6 8 x 4 = 5 8 x 5 = 4 8 x 6 = 3 8 x 7 = 2 8 x 8 = 1 8 x 9 = 9 | 1 x 1 = 1 1 x 2 = 2 1 x 3 = 3 1 x 4 = 4 1 x 5 = 5 1 x 6 = 6 1 x 7 = 7 1 x 8 = 8 1 x 9 = 9 | 7 x 1 = 7 7 x 2 = 5 7 x 3 = 3 7 x 4 = 1 7 x 5 = 8 7 x 6 = 6 7 x 7 = 4 7 x 8 = 2 7 x 9 = 9 | 2 x 1 = 2 2 x 2 = 4 2 x 3 = 6 2 x 4 = 8 2 x 5 = 1 2 x 6 = 3 2 x 7 = 5 2 x 8 = 7 2 x 9 = 9 | 5 x 1 = 5 5 x 2 = 1 5 x 3 = 6 5 x 4 = 2 5 x 5 = 7 5 x 6 = 3 5 x 7 = 8 5 x 8 = 4 5 x 9 = 9 | 4 x 1 = 4 4 x 2 = 8 4 x 3 = 3 4 x 4 = 7 4 x 5 = 2 4 x 6 = 6 4 x 7 = 1 4 x 8 = 5 4 x 9 = 9 |
order: 639 | order: 369 | order: 369 | order: 639 | order: 639 | order: 369 |
We will now show each number and the order of its series. This order, as you have just seen, was determined by the inner triangle of each series (the points of 3, 6 and 9 on the circle) and the number present at those points turns out to be either a sequence of 639 or 369. 639 represents energy moving counterclockwise and 369 is the energy moving clockwise. For purposes of demonstration, we will fix polarity designations to the 639 and 369. We will call 369 positive and 639 negative. The numbers 3,6 and 9, not being part of the periods, we will call neutral (=):
Note | Number | Order | Polarity |
C | 0 | = | |
D | 1 | 369 | + |
E | 2 | 639 | – |
(shock) | 3 | = | |
F | 4 | 369 | + |
G | 5 | 639 | – |
(shock) | 6 | = | |
A | 7 | 369 | + |
B | 8 | 639 | – |
C | 9 | = |
We will turn again to the sequences that we have created above. For simplicity’s sake, we will just use the forward sequence from each set. These sequences were: 123456789 (from 8-1), 135792468 (from 7-2) 639639639 (from 6-3) and 159483726 (from 5-4). Applying the polarities, we assigned in the chart above to these sequences we get:
8-1 | 1 2 3 4 5 6 7 8 9 |
+ – = + – = + – = | |
7-2 | 1 3 5 7 9 2 4 6 8 |
+ = – + = – + = – | |
6-3 | 6 3 9 6 3 9 6 3 9 |
(all neutral) | |
5-4 | 1 5 9 4 8 3 7 2 6 |
+ – = + – = + – = |
